考点:三角形面积与底的正比关系
专题:平面图形的认识与计算
分析:①由
××=1,得到G是BC中点,又因为F是DG中点,得出6对三角形面积等,又因为ABCD是平行四边形,所以S△
ABD=S△
BDC,因此图中有7对三角形的面积相等.
②根据①面积相等的三角形,得出
=
=
=3.再根据平行四边形面积是48,即可求出△FGC与△DEF的面积.
③图中阴影部分的面积是三角形FGC的面积,②已求出.
解答:
解:①由
××=1,得到G是BC中点,又因为F是DG中点,有6对三角形面积等,即:
S△
DCF=S△
GCF,S△
ABD=S△
BCD,S△
BDF=S△
BGF,S△
BDG=S△
CDG,S△
BFG=S△
GFC,
S△
FGC=S△
DFC,
又因为ABCD是平行四边形,所以S△
ABD=S△
BDC,
因此图中有7对三角形的面积相等.
②因为S△
DCF=S△
GCF,S△
ABD=S△
BCD,S△
BDF=S△
BGF,S△
BDG=S△
CDG,S△
BFG=S△
GFC,S△
FGC=S△
DFC,
所以
=
=
=3.
因为平行四边形面积是48,
所以S△
FGC=S△
FCD=
S△
DGC=
×
×48=6(平方厘米).
因为CE=2DE,所以S△
DEF=
S△
FCD=6×
=2(平方厘米).
③图中阴影部分的面积是三角形FGC的面积,即S△
FGC=6(平方厘米).
点评:此题考查了平行四边形的性质和三角形面积的求解方法.解题的关键是注意当两个三角形等底等高时面积相等.

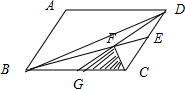 如图,平行四边形ABCD的面积是48cm2,CE=2DE,F是DG中点.
如图,平行四边形ABCD的面积是48cm2,CE=2DE,F是DG中点.