Question

在一个圆环形的跑道上，甲比乙快，甲、乙两人在同一地点沿相同方向跑时，每隔16分相遇一次，如果两人速度不变，两人在同一地点沿相反方向跑时，每隔8分相遇一次，则甲跑一圈需要________分，乙跑一圈需要________分．

Answer 1

10    32
分析：甲、乙两人相向而行，相遇一次是甲比乙多跑一圈是一个追赶问题，要去16分钟，则速度差是；而甲、乙两人相反方向而行，因为是圆环跑道上，则是相遇问题，要8分钟，两人的速度和是，快的速度就=（速度和+速度差）÷2．即（+）÷2=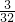．则跑一圈用用时间是1÷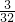=（分钟）=10（分钟），慢的速度就=（速度和-速度差）÷2即（-）÷2=，则跑一圈用时间是1÷=32分钟．故甲跑一圈要用10分钟，乙跑一圈则要用32分钟．
解答：由于甲、乙在圆环上跑步相向而行属于追赶问题，相反向而行是相遇问题从而我们可以知道两人速度之和则甲和乙的速度和是，速度差是
甲的速度就是（+）÷2=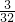，则跑一圈用时间是1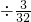=（分钟）=10（分钟）
乙的速度就是（-）÷2=，则跑一圈用时间是1÷=32（分钟）
答：甲跑一圈需要10分钟，乙跑一圈需要32分钟．
点评：本题我们要利用速度和与速度差的倍差关系来解决问题．