解答:解:(1)因为48能被3整除,所以“第十四届”所表示的数能被3整除,即“第14届”的四个数字之和能被3整除.
又因为1+3+5+…+9=45能被3整除,所以“华杯赛”表示的数的数字之和也能被3整除,即“华杯赛”所表示的数能被3整除.
(2)因为48能被4整除,而且“祝”字是4,“贺”字是8,所以“届”为偶数,只能取2或6.
又“祝贺”与“华杯赛”的成绩为四位数,所以“华”字代表的数字只能是1,否则,即使“华杯赛”取最小的三位数是213,48×213=10224是五位数,所以取其他的三位数将更不符合要求.
(3)当“届”取数字“2”时,则“赛”字只能是9,此时,算式是48×
=
.
因为余下的4个数字3,5,6,7中,只有5与10的和能被3整除,所以“杯”字只能取5.
此时,48×159=7632,符合要求.故“华杯赛”所代表的整数是159.
(4)当“届”取数字“6”时,则“赛”取数字“2”或“7”.
③若“赛”取数字“2”时,此时算式是48×
=
.
因为3与3,5,7,9的和分别为6,8,10,12,所以“杯”可以取数字“3”或“9”.
但是48×132=6336,48×192=9216,显然不符合要求.
④若“赛”取数字“7”时,此时算式是
=
.
因为8与2,3,5,9的和分别为10,11,13,17均不能被3整除,所以不存在“
”使得等式48×
=
成立.
所以“华杯赛”所代表的整数为159.

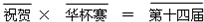 在如图所示的乘法算式中,汉字代表1至9这9个数字,不同汉字代表不同的数字.若“祝”字和“贺”字分别代表数字“4”和“8”,求出“华杯赛”所代表的整数.
在如图所示的乘法算式中,汉字代表1至9这9个数字,不同汉字代表不同的数字.若“祝”字和“贺”字分别代表数字“4”和“8”,求出“华杯赛”所代表的整数.


