Question

8．已知正方形ABCD的面积是30平方厘米，四边形GCEF为正方形，阴影部分的面积是15平方厘米

Answer 1

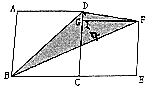
分析 如图，分别作AD、EF的延长线相交于点H，这样四边形DBEH是一个梯形．阴影部分面积造型这个梯形的面积减去三角形BEF的面积，再减去三角形DHF面积．根据三角形的面积计算公式“S=$\frac{1}{2}$ah”、梯形面积计算公式“S=$\frac{1}{2}$（a+b）h”，我们再设大正方形的边长为acm，小正方形的边长为bcm，即可解答．

解答 解：如图，分别作AD、EF的延长线相交于点H．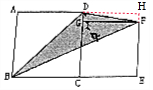

三角形BEF的面积：
$\frac{1}{2}$×（a+b）×b
三角形DHF的面积：
$\frac{1}{2}$×（a-b）×b
梯形DBEH的面积：
$\frac{1}{2}$×（b+a+b）×a
阴影部分面积：
$\frac{1}{2}$×（b+a+b）×b-$\frac{1}{2}$×（a+b）×b-$\frac{1}{2}$×（a-b）×b
=$\frac{1}{2}$×（a+2b）×a-$\frac{1}{2}$×（a+b）×b-$\frac{1}{2}$×（a-b）×b
=$\frac{1}{2}$a²
=$\frac{1}{2}$×30
=15（平方厘米）
答：阴影部分面积是15平方厘米．
故答案为：15平方厘米．

点评 此题难度较大．通过作辅助线，很容易看出阴影部分面积造型梯形面积减去两个三角形面积，没告诉大、小正方形的边长，只知道大正方形的面积，设大正方形的边长为acm，小正方形的边长为bcm，根据三角形面积计算公式、梯形面积计算公式，用含有字母a、b的式子表示三角形、梯形的面积，通过计算最后是$\frac{1}{2}$a²，a²已知，从而求阴影部分面积．