
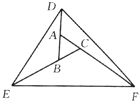
 如图,将三角形ABC的BA边延长1倍到D,CB的边延长2倍到E,AC边延长1倍到F,如果三角形ABC的面积等于1,那么三角形DEF的面积是( )
如图,将三角形ABC的BA边延长1倍到D,CB的边延长2倍到E,AC边延长1倍到F,如果三角形ABC的面积等于1,那么三角形DEF的面积是( )| A. | 10 | B. | 18 | C. | 9 | D. | 11 |
分析 连结AE、DC、BF,根据三角形面积与底的正比关系,分别求出三角形BDE、三角形ADF以及三角形CEF与三角形ABC之间的面积关系,解决问题.
解答 解:连结AE、DC、BF,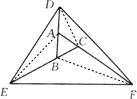
在△AEC中,因为BE=2BC,所以S△ABE=2S△ABC
又AB=AD,所以S△ABE=S△ADE
那么S△BDE=S△ABE+S△ADE=4S△ABC;
同理证得:S△ADF=4S△ABC,
S△CEF=8S△ABC.
因此S△BDE+S△ADF+S△CEF+SADC=4S△ABC+4S△ABC+8S△ABC+S△ABC=17S△ABC
所以S△DEC=17S△ABC+S△ABC=18S△ABC;
因为S△ABC=1,
所以S△DEC=18.
答:三角形DEF的面积是18.
故选:B.
点评 此题充分运用了三角形面积与底的正比关系,求出各三角形与三角形ABC之间的面积关系,进而解决问题.


 优生乐园系列答案
优生乐园系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com