Question

把一些棱长为1的正方体粘成一个棱长为n（n为正整数）的实心正方体，将大正方体的一个或几个面染成红色，然后再将大正方体拆散，发现有281个小正方体被染色了，那么n=

9

．

Answer 1

分析：三面涂色的只有8个顶点，两面涂色的是12条棱上除去顶点的部分，一面涂色的是比棱长少2的正方形，据此计算即可解答．

解答：解：我们把大正方体分为上、下，前、后，左、右六个面．
1．如果只染一个面，只染大正方体的上面，那么，被染色的小正方体的块数应为n²个，因为281是质数，不是一个完全平方数，所以不可能是染一个面．
2．如果将大正方体的两个面染成红色有两种情况．
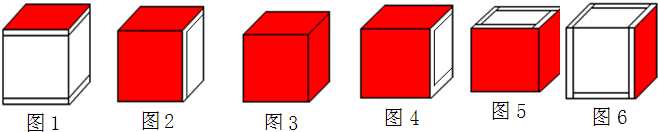
  ①染上下两个面（两个面相对），如图1，这时被染色的小正方体的块数应为2n²个，这也是不可能的．
②染上面和前面两个面（两个面相邻），如图2，这时这时被染色的小正方体的块数应为：2 n²-n=n×（2n-1），因为281是质数，所以n×（2n-1）不可能等于281．

3．如果将大正方体的三个面染成红色，有如下两种情况
①染上面、前面和右面，如图3，这时被染色的小正方体的块数应为n³-（n-1）³，n³-（n-1）³应是被3除余1的数，这是因为：

n被3除的余数	0	1	2
n 3被3除的余数	0	1	2
（n-1）被3除的余数	2	0	1
（n-1）3被3除的余数	2	0	1
n3-（n-1）3被3除的余数	1	1	1

因为281 被3除余2，所以n ³-（n-1）³不可能等于281．（或被染色的小正方体的块数，还可以表示为3n²-3n+1=281，那么3n ²-3n=280，因为280不是3的倍数，所以也不合题意）．
②染上面、前面和下面，如图4，这时被染色的小正方体的块数应为：
3n²-2n=n×（3n-2），因为281是质数，所以n×（3n-2）不可能等于281．
4．如果将大正方体的四个面染成红色，有如下两种情况
①上、下两个面不染色，如图5，把被染上红色的小正方体切分成弦图那样，这时，被染上红色的小正方体块数应为4的倍数，而281不是4的倍数，不合题意．
②上面和前面不染色，如图6，这时被染色的小正方体的块数为：
2n²+n×（n-2）+（n-2）×（n-1）=4n²-5n+2
4n²-5n+2=281
4n²-5n=279
n×（4n-5）=279
因为279=1×179=3×91=9×31，经试验只有当n=9时，才符合要求．
5．如果将大正方体的五个面染上红色，如上面不染色，这时被染色的小正方体的块数为：2n²+2n（n-2）+（n-2）×（n-2）=5n²-8n+4
如果5 n²-8n+4=281，那么5 n²-8n=277，n×（5n-8）=277，由于277是质数，所以n没有符合题意的解．
 6．如果将大正方体的六个面都染上红色，这时被染色的小正方体的块数为：
n³-（n-2）³
由于n与n-2是同奇偶的，所以n³与（n-2）³也应是同奇偶的，同奇偶的两个
数的差应为偶数，而281是奇数，所以n³-（n-2）³不可以等于281，不符合题意．
综上所述，只有当n=9；有两个相邻的面不染色时，才符合题目要求．所以n=9．
故答案为：9．

点评：根据立体图形的知识可知：三个面均为红色的是各顶点处的小正方体，在各棱处，除去顶点处的正方体的有两面红色，在每个面上，除去棱上的正方体都是一面红色，所有的小正方体的个数减去有红色的小正方体的个数即是没有涂色的小正方体．