Question

6．如图是两个正方形，如果两块阴影部分的面积之比是8，那么大正方形面积是小正方形多少倍？

Answer 1

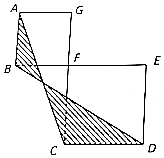
分析 可设两个正方形的边长分别是a，b，根据相似三角形的性质可得两块阴影部分的面积之比为$\frac{{a}^{3}}{{b}^{3}}$，根据已知条件可求$\frac{{a}^{3}}{{b}^{3}}$=8，进一步得到$\frac{a}{b}$=2，依此可得大正方形面积是小正方形多少倍．

解答 解：设两个正方形的边长分别是a，b，则两块阴影部分的面积之比为
$\frac{OA}{OD}$×$\frac{OB}{OC}$=$\frac{AM}{CD}$×$\frac{AB}{CN}$=$\frac{CE×\frac{AB}{BE}}{CD}$×$\frac{AB}{AE×\frac{CD}{DE}}$=$\frac{a×\frac{a}{a+b}}{b}$×$\frac{a}{b×\frac{b}{a+b}}$=$\frac{{a}^{3}}{{b}^{3}}$，
因为两块阴影部分的面积之比是8，
所以$\frac{{a}^{3}}{{b}^{3}}$=8，
所以$\frac{a}{b}$=2，
所以$\frac{{a}^{2}}{{b}^{2}}$=4．
答：大正方形面积是小正方形4倍．

点评 考查了组合图形的面积，本题主要是熟悉相似三角形的性质，得到大正方形和小正方形边长的比．