Question

求如图各涂色部分的面积．（单位：cm）

Answer 1

考点：组合图形的面积

专题：平面图形的认识与计算

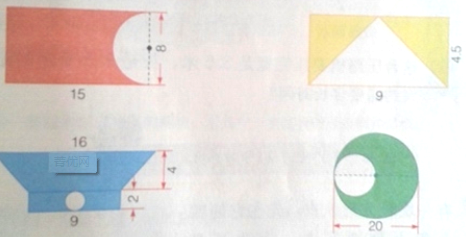
分析：（1）涂色部分的面积=长方形的面积-直径为8厘米半圆的面积；根据长方形、圆的面积公式解答即可．
（2）涂色部分的面积=长方形的面积-空白三角形的面积；根据长方形、三角形的面积公式解答即可．
（3）涂色部分的面积=梯形的面积+长方形的面积-圆的面积；圆的直径为2厘米；根据梯形、长方形、圆的面积公式解答即可．
（4）涂色部分的面积=大圆的面积-小圆的面积；根据圆的面积公式解答即可．

解答： 解：（1）15×8-

1

2

×3.14×（8÷2）²
=120-25.12
=94.88（平方厘米）
答：涂色部分的面积是94.88平方厘米．

（2）9×4.5-9×4.5÷2
=40.5-20.25
=20.25（平方厘米）
答：涂色部分的面积是20.25平方厘米．

（3）（9+16）×4÷2+9×2-3.14×（2÷2）²
=25×4÷2+18-3.14×1
=50+18-3.14
=64.86（平方厘米）
答：涂色部分的面积是64.86平方厘米．

（4）3.14×（20÷2）²-3.14×（20÷2÷2）²
=3.14×100-3.14×25
=314-78.5
=235.5（平方厘米）
答：涂色部分的面积是235.5平方厘米．

点评：此题考查组合图形面积的计算方法，一般都是转化到规则图形中利用面积公式计算解答．