
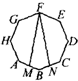
 如图,正八边形ABCDEFGH的面积为32平方厘米,M、N分别为AB、BC的中点,则四边形MBNF的面积为
如图,正八边形ABCDEFGH的面积为32平方厘米,M、N分别为AB、BC的中点,则四边形MBNF的面积为| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
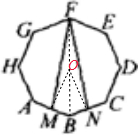 解:如图所示:连接点F和B,找出FB的中点O即是正八边形ABCDEFGH的中心,然后连接OM、ON;
解:如图所示:连接点F和B,找出FB的中点O即是正八边形ABCDEFGH的中心,然后连接OM、ON;| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:小学数学 来源: 题型:
 如图是一个八边形点阵,中心一个点算是第一层,第二层每边两个点(八边形顶点处有一点为相邻两边公用),第三层每边三个点,第四层每边四个点,其余类推,若八边形点阵共有10层,则点阵中点的总数是
如图是一个八边形点阵,中心一个点算是第一层,第二层每边两个点(八边形顶点处有一点为相邻两边公用),第三层每边三个点,第四层每边四个点,其余类推,若八边形点阵共有10层,则点阵中点的总数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com