
 ABCD是边长12厘米的正方形,E、F分别是AB、BC边的中点,AF与CE交于G,则四边形AGCD的面积=________平方厘米.
ABCD是边长12厘米的正方形,E、F分别是AB、BC边的中点,AF与CE交于G,则四边形AGCD的面积=________平方厘米. =
=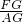 =
=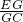 =0.5,因为等高三角形面积比等于底边比,所以S△GEF:S△GEA=0.5,又因为S△GEF+S△GEA=S△AEF=0.5S△ABF=S△BEF=18(平方厘米),所以S△GEF=
=0.5,因为等高三角形面积比等于底边比,所以S△GEF:S△GEA=0.5,又因为S△GEF+S△GEA=S△AEF=0.5S△ABF=S△BEF=18(平方厘米),所以S△GEF= S△AEF=6(平方厘米),S四边形ABCG=S△AEF+S△BCE-S△GEF=18+36-6=48(平方厘米),所以S四边形AGCD=S正方形ABCD-S四边形ABCG=144-48=96(平方厘米).
S△AEF=6(平方厘米),S四边形ABCG=S△AEF+S△BCE-S△GEF=18+36-6=48(平方厘米),所以S四边形AGCD=S正方形ABCD-S四边形ABCG=144-48=96(平方厘米). 解:如图,S正方形=12×12=144(平方厘米),
解:如图,S正方形=12×12=144(平方厘米), =
=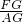 =
=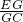 =0.5,
=0.5, S△AEF=6(平方厘米),
S△AEF=6(平方厘米),

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:小学数学 来源: 题型:
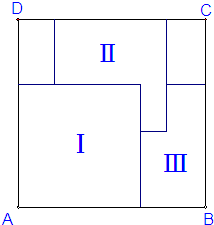 如图,三个大小相同的正方形重叠地放在一个大的正方形ABCD内,已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形ABCD的边长是
如图,三个大小相同的正方形重叠地放在一个大的正方形ABCD内,已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形ABCD的边长是查看答案和解析>>
科目:小学数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com