Question

（1）以O为圆心画一个直径为4厘米的圆；
（2）在这个圆内画出一个最大的正方形；
（3）正方形的面积与圆的面积比是________；
（4）画出你所画的这个图形的所有对称轴．

Answer 1

解：据（1）、（2）、（4）的分析画图如下：
，
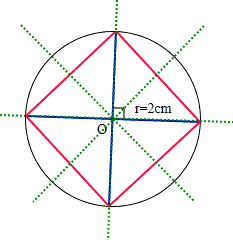
（3）正方形的面积为：4×（4÷2）÷2×2=8（平方厘米），
圆的面积为：3.14×（4÷2）²=12.56（平方厘米），
正方形的面积：圆的面积=8：12.56=100：157；
答：正方形的面积与圆的面积比是100：157．
故答案为：100：157．
分析：（1）由题意知，要画一个直径是4厘米的圆，首先确定圆的半径为4÷2=2厘米，再依据画圆的方法画一个圆即可．
（2）由题意可知：这个最大正方形的对角线应等于圆的直径，因此可以画两条互相垂直的直径，依次连接两条直径的4个端点，即可完成作图．
（3）因为这个最大正方形的对角线等于圆的直径，所以利用正方形和圆的面积公式即可求出正方形和圆的面积比．
（4）依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，这条直线就是其对称轴，于是即可画出这个图形的对称轴．
点评：（1）解答此题要明确半径是2厘米，即画圆时圆规两脚叉开的距离为2厘米．
（2）解答此题的关键是明白：这个最大正方形的对角线应等于圆的直径，据此即可画出符合要求的正方形．
（3）此题主要考查正方形和圆的面积的计算方法，关键是明白：这个最大正方形的对角线等于圆的直径．
（4）此题主要考查轴对称图形的意义及其对称轴的条数．