
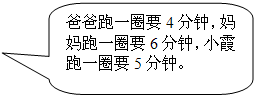
 (1)如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇?此时爸爸、妈妈分别跑了多少圈?
(1)如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇?此时爸爸、妈妈分别跑了多少圈? ,妈妈每分钟跑1圈的
,妈妈每分钟跑1圈的 ,爸爸每分钟比妈妈多跑1圈的(
,爸爸每分钟比妈妈多跑1圈的(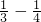 )=
)= ,爸爸妈妈同时起跑,到再次相遇,爸爸要比妈妈多跑1圈,所以爸爸比妈妈多跑1圈的时间为:
,爸爸妈妈同时起跑,到再次相遇,爸爸要比妈妈多跑1圈,所以爸爸比妈妈多跑1圈的时间为: =12(分)(追及问题:路程差÷速度差=追及时间);此时,爸爸跑了12÷4=3(圈),妈妈跑了12÷6=2(圈).
=12(分)(追及问题:路程差÷速度差=追及时间);此时,爸爸跑了12÷4=3(圈),妈妈跑了12÷6=2(圈). 

 阅读快车系列答案
阅读快车系列答案科目:小学数学 来源: 题型:填空题
 ,玲玲用小棒搭房子,她搭3间房子用13根小棒.照这样,搭8间房子要用________根小棒;搭n间房子要用________根小棒.(用含有n的式子表示)
,玲玲用小棒搭房子,她搭3间房子用13根小棒.照这样,搭8间房子要用________根小棒;搭n间房子要用________根小棒.(用含有n的式子表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com