
 小花猫和小花狗是一对好朋友,他们分别从A、B两地同时出发,相向而行,小花猫每分钟行80米,小花狗每分钟行100米,他们在途中C处相遇.问:A、B两地之间的距离是多少米?
小花猫和小花狗是一对好朋友,他们分别从A、B两地同时出发,相向而行,小花猫每分钟行80米,小花狗每分钟行100米,他们在途中C处相遇.问:A、B两地之间的距离是多少米?
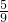 ,于是C和中点的距离占AB全程的
,于是C和中点的距离占AB全程的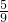 -
- =
=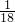 ,则全程距离是:120÷
,则全程距离是:120÷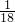 =2160米.
=2160米.

科目:小学数学 来源: 题型:
 小花猫和小花狗是一对好朋友,他们分别从A、B两地同时出发,相向而行,小花猫每分钟行80米,小花狗每分钟行100米,他们在途中C处相遇.问:A、B两地之间的距离是多少米?
小花猫和小花狗是一对好朋友,他们分别从A、B两地同时出发,相向而行,小花猫每分钟行80米,小花狗每分钟行100米,他们在途中C处相遇.问:A、B两地之间的距离是多少米?查看答案和解析>>
科目:小学数学 来源: 题型:
 小花猫和小花狗是一对好朋友,它们分别从甲、乙两地同时出发,相向而行.小花猫到达乙地立即返回甲地,小花狗到达甲地后立即返回乙地,于是它们在距第一次相遇的地方204米处第二次相遇.问:甲、乙两地之间的距离是多少米?
小花猫和小花狗是一对好朋友,它们分别从甲、乙两地同时出发,相向而行.小花猫到达乙地立即返回甲地,小花狗到达甲地后立即返回乙地,于是它们在距第一次相遇的地方204米处第二次相遇.问:甲、乙两地之间的距离是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com