
分析 首先根据工作效率=工作量÷工作时间,分别求出两个进水管的工作效率,进而求出它们的工作效率之和是多少;然后根据工作量=工作效率×工作时间,用甲乙的工作效率之和乘以8,求出两个进水管8分钟可以注水多少,用它减去1,再除以1号水管的工作效率,求出1号水管单独注水的时间最长是多少;最后用8减去1号水管单独注水的时间,求出两个水管至少应同时打开多长时间即可.
解答 解:8-[($\frac{1}{15}+\frac{1}{10}$)×$8-1]÷\frac{1}{15}$$÷\frac{1}{15}$
=8-[$\frac{4}{3}$-1]×15
=$8-\frac{1}{3}×15$
=8-5
=3(分钟)
答:两个水管至少应同时打开3分钟.
点评 此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率;解答此题的关键是求出1号水管单独注水的时间最长是多少.


科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
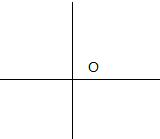 如图是两条互相垂直的直线,相交于O点.
如图是两条互相垂直的直线,相交于O点.查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com