
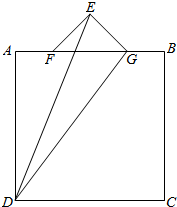
 在图中,ABCD为边长为12的正方形,三角形EFG为一个等腰直角三角形,其中E为直角顶点,F和G为AB的四等分点.即AB=4AF=4BG,求三角形EGD的面积是多少?
在图中,ABCD为边长为12的正方形,三角形EFG为一个等腰直角三角形,其中E为直角顶点,F和G为AB的四等分点.即AB=4AF=4BG,求三角形EGD的面积是多少? 分析 如图,连接AE,因为F和G为AB的四等分点,又因为AB=4AF=4BG,所以FG=$\frac{1}{2}$AB,然后求出三角形AGE、三角形AGD以及三角形ADE的面积,再根据S△DEG=S△AGE+S△AGD-S△ADE,解决问题.
解答 解:连接AE,
因为F和G为AB的四等分点,又因为AB=4AF=4BG,
所以FG=$\frac{1}{2}$AB,
所以S△AGE=$\frac{1}{2}$AG×$\frac{1}{2}$FG=$\frac{1}{4}$×$\frac{3}{4}$AB×$\frac{1}{2}$AB=$\frac{3}{32}$×12×12=13.5,
S△AGD=$\frac{1}{2}$AG×AD=$\frac{1}{2}$×$\frac{3}{4}$×AB×AB=54,
S△ADE=$\frac{1}{2}$AD×AB=$\frac{1}{2}$×12×$\frac{1}{2}$×12=36,
所以S△DEG=S△AGE+S△AGD-S△ADE=13.6+54-36=31.5.
点评 此题解答的关键在于作出辅助线,根据F和G为AB的四等分点,求出FG=$\frac{1}{2}$AB,再根据三角形面积与边的关系,求出相关三角形的面积,解决问题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:小学数学 来源: 题型:解答题
| $\frac{1}{2}$÷$\frac{5}{4}$÷$\frac{2}{15}$ | ($\frac{7}{9}$+$\frac{5}{27}$)×54 | ($\frac{5}{8}$+$\frac{3}{8}$×$\frac{2}{3}$)÷$\frac{7}{16}$ |
| $\frac{5}{6}$×$\frac{7}{8}$+$\frac{5}{6}$×$\frac{1}{8}$ | $\frac{3}{85}$×86 | 3.7×120%+1.3×1.2. |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com