


科目:小学数学 来源:数学教研室 题型:072
议一议
(1)
正六边形能否密铺?简述你的理由。(2)
分析图,讨论正五边形不能密铺的原因。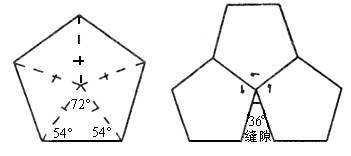
(3)
还能找到能密铺的其他正多边形吗?通过上述问题的探讨研究,可以看出对于给定的某种正多边形,它能否拼成一个平面图形,既不留下一丝空白,又不相互重叠,显然与它的内角大小有关。为了探索哪些正多边形能铺满平面,请根据图,用计算器或量角器完成下表:

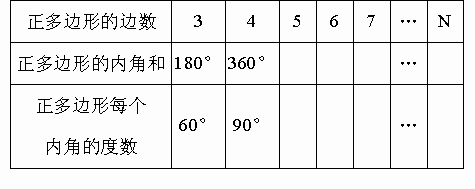
通过上面研讨和计算,我们可以发现:当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。
如正六边形的每个内角为
120°,三个120°拼在一起恰好组成周角,所以全用正六边形瓷砖就可以铺满地面。所以用相同的正多边形拼地板或用两种以上的正多边形拼地板都可以达到密铺的目的,甚至一些不规则的图形也可以做到,如图所示。
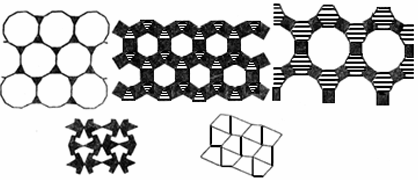
通过这节的学习,你学到了哪些知识,有哪些收获,能否运用你所学过的知识试着完成下列问题。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com