
 化成小数,那么小数点后的第1993位的数字是________,此1993个数字之和等于________.
化成小数,那么小数点后的第1993位的数字是________,此1993个数字之和等于________. 化成小数是
化成小数是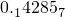 ,循环节是6位数,然后用1993除以6,看看余数是几,然后看看这位上的数字是几,即可判断出第1993位的数字是多少;
,循环节是6位数,然后用1993除以6,看看余数是几,然后看看这位上的数字是几,即可判断出第1993位的数字是多少; =
=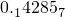 ,1993÷6=332…1.因为循环节的第一位数字是1,故第1993位是1;
,1993÷6=332…1.因为循环节的第一位数字是1,故第1993位是1;

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com