
分析 设相遇所用时间为t,甲速度为3x千米/小时,乙速度为2x千米/小时,2xt+3xt=东、西两村总路程,也就是说总路程是5xt千米.因为乙走了2xt所以他距东村就还有3xt千米的路程.同样甲距西村有2xt千米的路程. 然后根据当“到达西村时,乙离东村还有14千米”可以用时间相等得到一个等式,即可列方程求解.
解答 解:设两地距离是skm,甲速度为3x千米/小时,乙速度为2x千米/小时;
第一次相遇时甲乙所走的路程分别为$\frac{2}{3+2}$s=0.6s(km),$\frac{2}{3+2}$s=0.4s(km);
根据相遇后甲到B地所用时间列方程:
$\frac{0.4s}{3x(1+20%)}$=$\frac{0.6s-14}{2x(1+30%)}$
0.4s×2x(1+30%)=(0.6x-14)×3x(1+20%)
0.4s×2.6=(0.6s-14)×3.6
1.04s=2.16s-50.4
1.12s-50.4=0
1.12s=50.4
s=45.
答:东、西两村相距45千米.
点评 本题主要考查了列方程解应用题中的行程问题,正确理解速度、时间、路程之间的关系,把当到达西村时,乙离东村还有14千米,转化为相等关系是解题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:小学数学 来源: 题型:解答题
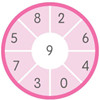 在这个投掷飞镖的圆靶上,有(5)种方法可以只用四支飞镖得到25分,每支飞镖都要打到圆靶上,并且不能掉落到地板上.每组数字只能用一次,改变顺序则不算.
在这个投掷飞镖的圆靶上,有(5)种方法可以只用四支飞镖得到25分,每支飞镖都要打到圆靶上,并且不能掉落到地板上.每组数字只能用一次,改变顺序则不算.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com