
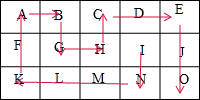
 在3×5的棋盘上,一个棋子每次可以沿水平或竖直方向移动一小格,但不可以沿任何斜对角线移动.从某些特定的格子开始,要求棋子经过全部的小正方格恰好一次,但不须回到原来出发的小方格上.在这15个小方格中,则有
在3×5的棋盘上,一个棋子每次可以沿水平或竖直方向移动一小格,但不可以沿任何斜对角线移动.从某些特定的格子开始,要求棋子经过全部的小正方格恰好一次,但不须回到原来出发的小方格上.在这15个小方格中,则有




 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:小学数学 来源: 题型:
 在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子只能向前或向右翻动.开始时,骰子如图1那样摆放,朝上的点数是2;最后翻动到如图2所示的位置.此时,骰子朝上的点数不可能是下列选项中的( )
在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子只能向前或向右翻动.开始时,骰子如图1那样摆放,朝上的点数是2;最后翻动到如图2所示的位置.此时,骰子朝上的点数不可能是下列选项中的( )查看答案和解析>>
科目:小学数学 来源: 题型:单选题
 在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子只能向前或向右翻动.开始时,骰子如图1那样摆放,朝上的点数是2;最后翻动到如图2所示的位置.此时,骰子朝上的点数不可能是下列选项中的
在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子只能向前或向右翻动.开始时,骰子如图1那样摆放,朝上的点数是2;最后翻动到如图2所示的位置.此时,骰子朝上的点数不可能是下列选项中的查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com