Question

数学小博士．
（1）比一比，谁的面积大，用“√”标出．

（2）你能算出阴影部分的面积吗？

Answer 1

考点：面积及面积的大小比较

专题：平面图形的认识与计算

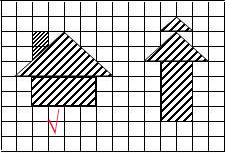
分析：（1）假设每个小正方形的边长为1厘米，分别计算出每个图形的面积，即可比较大小；左图的面积为长6厘米、宽2厘米的长方形的面积加上底8厘米、高3厘米的三角形的面积再加上上底1厘米、下底2厘米、高1厘米的梯形的面积；右图的面积为底为2厘米、高1厘米的三角形的面积加上底4厘米、高2厘米的三角形的面积再加上长4厘米、宽2厘米的长方形的面积．利用长方形、三角形和梯形的面积公式，代入数据求出即可．
（2）观察图形可知，阴影部分的面积等于长为100米、宽为60米的长方形的面积减去长为100-30=70米、宽为60-20=40米的长方形的面积．

解答： 解：（1）假设每个小正方形的边长为1厘米，
则左图的面积为：
4×2+6×3÷2+（1+2）×1÷2
=8+9+1.5
=18.5（平方厘米），
右图的面积：4×2+4×2÷2+2×1÷2
=8+4+1
=13（平方厘米），
因为18.5＞13，
所以左图的面积大；

（2）100×60-（100-30）×（60-20）
=600-280
=320（平方米），
答：阴影部分的面积是320平方米．
故答案为：（1）

点评：（1）分别计算出每个图形的面积，是解答本题的关键．（2）关键是善于利用规则图形的面积的和差来求出不规则图形的面积．