Question

计算下列图1图2阴影部分面积．

Answer 1

考点：组合图形的面积

专题：平面图形的认识与计算

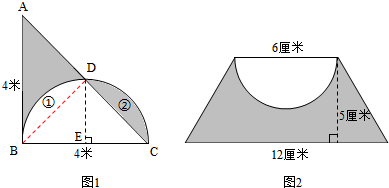
分析：（1）如图所示：图1中，三角形ABC是等腰直角三角形，连接BD，则三角形BDE和三角形CDE都是等腰直角三角形，所以空白①的面积就等于阴影②的面积，由此可以得出，阴影部分的面积就等于三角形ABC的面积的一半，据此解答即可；
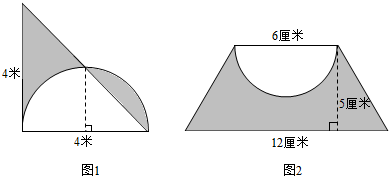
（2）阴影部分的面积=梯形的面积-半圆的面积，据此代入数据即可求解．

解答： 解：（1）4×4÷2÷2
=16÷2÷2
=4（平方米）
答：阴影部分的面积是4平方米．

（2）（6+12）×5÷2-3.14×（6÷2）²÷2
=18×5÷2-3.14×9÷2
=45-14.13
=30.87（平方厘米）
答：阴影部分的面积是30.87平方厘米．

点评：解答此题的关键是：弄清楚阴影部分的面积可以由哪些图形的面积和或差进行求解．