解:(1)在一个分数中,如果分母加上或减去某个数后,在不约分的情况下,不变量是分子;
(2)在一个分数中,如果分子加上或减去某个数后,在不约分的情况下,不变量是分母;
(3)在一个分数中,如果分子减去某个数,分母加上某个数,在不约分的情况下,不变量是分子与分母的和;
(4)在一个分数中,如果分子分母同减去某个数,在不约分的情况下,不变量是分子与分母的差;
(5)在一个分数中,如果分子分母同加某个数,在不约分的情况下,不变量是分子与分母的差.
故答案为:(1)分子;(2)分母;93)分子与分母的和;(4)分子与分母的差;(5)分子与分母的差.
分析:假设分数的分子为a,分母为b,某个数为x,则:
(1)原分数为

,分母加上或减去某个数,不约分,变化的只是分母,分子不变;
(2)原分数为

,分子加上或减去某个数,不约分,变化的只是分子,分母不变;
(3)原分数为

,分子减去某个数,分母加上某个数,则变成
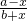
,则分子分母的和为:a-x+b+x=a+b,原分数分子与分母的和也是a+b,所以不变量是分子与分母的和;
(4)原分数为

,分子分母同减去某个数,则变成
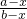
,则分子分母的差为:a-x-(b-x)=a-x-b+x=a-b,原分数分子与分母的差也是a-b,所以不变量是分子与分母的差;
(5)原分数为

,分子分母同加某个数,
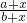
,分子分母的差为:a+x-(b+x)=a+x-b-x=a-b,原分数分子与分母的差也是a-b,所以不变量是分子与分母的差.
点评:解决本题要根据分子分母之间的变化与联系来解答.

 ,分母加上或减去某个数,不约分,变化的只是分母,分子不变;
,分母加上或减去某个数,不约分,变化的只是分母,分子不变; ,分子加上或减去某个数,不约分,变化的只是分子,分母不变;
,分子加上或减去某个数,不约分,变化的只是分子,分母不变; ,分子减去某个数,分母加上某个数,则变成
,分子减去某个数,分母加上某个数,则变成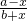 ,则分子分母的和为:a-x+b+x=a+b,原分数分子与分母的和也是a+b,所以不变量是分子与分母的和;
,则分子分母的和为:a-x+b+x=a+b,原分数分子与分母的和也是a+b,所以不变量是分子与分母的和; ,分子分母同减去某个数,则变成
,分子分母同减去某个数,则变成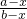 ,则分子分母的差为:a-x-(b-x)=a-x-b+x=a-b,原分数分子与分母的差也是a-b,所以不变量是分子与分母的差;
,则分子分母的差为:a-x-(b-x)=a-x-b+x=a-b,原分数分子与分母的差也是a-b,所以不变量是分子与分母的差; ,分子分母同加某个数,
,分子分母同加某个数,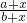 ,分子分母的差为:a+x-(b+x)=a+x-b-x=a-b,原分数分子与分母的差也是a-b,所以不变量是分子与分母的差.
,分子分母的差为:a+x-(b+x)=a+x-b-x=a-b,原分数分子与分母的差也是a-b,所以不变量是分子与分母的差.

 (2013?海淀区模拟)操作计算.
(2013?海淀区模拟)操作计算.