练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    4前面一个数是
     
    ，后面一个数是
     
    ．
    分析：根据相邻的两个整数相差1，依次进行计算即可．
    解答：解：4前面的一个数是：4-1=3，
    4后面一个数是：4+1=5，
    故答案为：3，5．
    点评：此题要明确：相邻的两个整数相差1，然后根据要求，即可算出结果．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

    在纸上写着一列自然数1，2，…，98，99．一次操作是指将这列数中最前面的三个数划去，然后把这三个数的和写在数列的最后面．例如第一次操作后得到4，5，…，98，99，6；而第二次操作后得到7，8，…，98，99，6，15．这样不断进行下去，最后将只剩下一个数，最初的99个数连同后面写下的数，纸上出现的所有数的总和是
    25128
    25128
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    在纸上写着一列自然数1，2，…，98，99．一次操作是指将这列数中最前面的三个数划去，然后把这三个数的和写在数列的最后面．例如第一次操作后得到4，5，…，98，99，6；而第二次操作后得到7，8，…，98，99，6，15．这样不断进行下去，最后将只剩下一个数，则最后剩下的数是
    4950
    4950
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：071

    数学兴趣小组上，老师出了下面几道题：

    1÷13

    1÷6

    4÷7

    让同学们判断各题的商是什么数，商最多除到多少位就开始循环．

    小明很快就得出，它们的商都是循环小数，商最多除到与除数相等的次数，就开始循环．同学们对这个答案都迷惑不解．你知道是为什么吗？

    其实，小明说的是对的，我们举例说明1÷13的竖式计算过程如下：

    每次除后，余数必须小于13，因此每次的余数只能是1～12中的一个．当除到第13次时，这次的余数应该是前面12个数中的某一个，也就是说最多除到第13位时，余数总会与前面的某个余数相同，而余数一相同，商就开始循环．所以，两个数相除，如果除不尽，最多除到与除数相等的次数，商就开始循环了．

    查看答案和解析>>

    科目：小学数学 来源：数学教研室 题型：072

    数学兴趣小组上，老师出了下面几道题：

    1÷13

    1÷6

    4÷7

    让同学们判断各题的商是什么数，商最多除到多少位就开始循环．

    小明很快就得出，它们的商都是循环小数，商最多除到与除数相等的次数，就开始循环．同学们对这个答案都迷惑不解．你知道是为什么吗？

    其实，小明说的是对的，我们举例说明1÷13的竖式计算过程如下：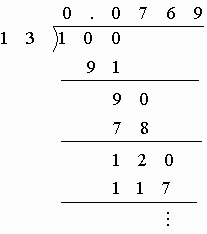

    每次除后，余数必须小于13，因此每次的余数只能是1～12中的一个．当除到第13次时，这次的余数应该是前面12个数中的某一个，也就是说最多除到第13位时，余数总会与前面的某个余数相同，而余数一相同，商就开始循环．所以，两个数相除，如果除不尽，最多除到与除数相等的次数，商就开始循环了．

    查看答案和解析>>

    科目：小学数学 来源：数学教研室 题型：072

    对策问题

    　　在数学竞赛中，有一类很有趣味的智办游戏题，涉及到的课本知识并不多，但是技巧性比较强。在智力游戏中，对立者总是竭尽全力争取最大的胜利，不希望自己失败，因此对立者都认真选择对付对方的方法。用数学的观点和方法来研究取胜的策略叫做对策问题。

    　　提问　在黑板上写下一列自然数2，3，4，5，…，1993，1994，甲先擦去其中一个数，然后乙再擦去一个数，如此轮流地擦下去，若最后剩下两个互质数时，甲取胜，若最后剩下两个不是互质数时，乙取胜，这个游戏中谁取胜的可能性最大?

    　　解　在2，3，4，5，…，1993，1994这一列数中，共有997个偶数，996个奇数，而且这一列数都是连续的自然数。大家知道，相邻的两个自然数一定是互质数。如果甲先擦去一个偶数2，就还剩下996个偶数和996个奇数，这时乙擦去某一个奇数时，甲就擦去其相邻后面的那个偶数，乙擦去某一个偶数时，甲就擦去其相邻前面的那个奇数，如此这般地擦995次后，就只剩下相邻的一奇数一偶数，它们必是互质数，甲必胜。

    查看答案和解析>>

    同步练习册答案