
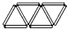
 ,照这样摆下去,摆10个三角形需21根小棒,摆n个三角形需2n+1根小棒.
,照这样摆下去,摆10个三角形需21根小棒,摆n个三角形需2n+1根小棒. 分析 摆一个三角形需3根小棒;
摆二个三角形需5根小棒;
摆三个三角形时需要7根小棒;
摆四个三角形时需要9根小棒;
…
第一个三角形需要3根小棒,以后每增加1个三角形就需要增加2根小棒;
当有n个三角形时小棒的数量就是3+2(n-1),然后化简,找出小棒的根数与与三角形个数直接的关系,进而求出摆10个三角形需多少根小棒.
解答 解:当有n个三角形时小棒的数量就是:
3+2(n-1)
=3+2n-2
=2n+1
摆10个三角形需:
2n+1
=2×10+1
=20+1
=21(根)
故答案为:21,2n+1.
点评 解决本题关键是找出小棒的数量随三角形的数量变化的规律,写出通项公式,进而求解.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com