Question

2．如图，在等腰直角角形ABC中，∠1=30°，∠2等于多少度？

Answer 1

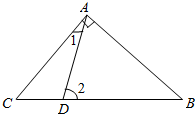
分析 三角形ABC是等腰三角形，而∠CAB是一个直角，90°，那么两个底角就分别是45°；∠1=30°，用90°减去∠1的度数，得出∠DAB的度数，再根据三角形的内角和是180°，在△ADB中，两个内角已知，用180°减去已知的这两个角，就是∠2的度数．

解答 解：∠B=（180°-90°）÷2
=90°÷2
=45°；
∠DAB=∠CAB-∠1=90°-30°=60°；
∠2=180°-60°-45°
=120°-45°
=75°．
答：∠2等于75°．

点评 解决本题要熟练掌握等腰三角形的特点，以及三角形的内角和定理．