Question

求下面图形的表面积和体积（单位：厘米）．

Answer 1

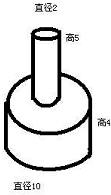
考点：规则立体图形的表面积,规则立体图形的体积

专题：立体图形的认识与计算

分析：（1）根据圆柱的表面积公式求出大圆柱的表面积，然后再加上小圆柱的侧面积即可求出组合图形的表面积；
（2）根据圆柱的体积公式分别求出大小圆柱的体积，然后求和即可求出组合图形的体积．

解答： 解：（1）大圆柱的表面积是：
2×3.14×（10÷2）²+3.14×10×4
=157+125.6
=282.6（平方厘米）
小圆柱的侧面积是：
3.14×2×5
=3.14×10
=31.4（平方厘米）
组合图形的表面积是：
282.6+31.4=314（平方厘米）

（2）组合图形的体积是：
3.14×（10÷2）²×4+3.14×（2÷2）²×5
=3.14×25×4+3.14×1×5
=314+15.7
=329.7（立方厘米）
答：表面积是314平方厘米，体积是329.7立方厘米．

点评：此题主要考查了根据圆柱的表面积和体积公式求组合图形的表面积和体积的方法．