
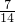 ×7+4x=7x-
×7+4x=7x-
 :
: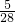 =(x-28):
=(x-28): .
.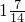 ×7+4X=7X-
×7+4X=7X- ,
, +4X=7X-
+4X=7X- ,
, =
= ,
, ,
,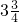 ;
; :
: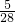 =(X-28):
=(X-28): ,
,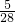 (X-28)=
(X-28)= ×
× ,
,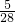 X-5=
X-5= ,
,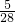 X=
X= ,
,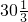 .
.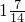 ×7,得出
×7,得出 +4X=7X-
+4X=7X- ,根据等式的基本性质,方程的两边同时减去4X得到3x-
,根据等式的基本性质,方程的两边同时减去4X得到3x- =
= ,再方程的两边同时加上
,再方程的两边同时加上 得3X=
得3X= ,方程两边再同时除以3来解;
,方程两边再同时除以3来解;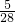 (X-28)=
(X-28)= ×
× ,先分别算出两边的得数,得出
,先分别算出两边的得数,得出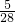 X-5=
X-5= ,利用等式的基本性质方程的两边同时加上5,得出
,利用等式的基本性质方程的两边同时加上5,得出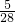 X=
X= ,再在方程两边同时除以
,再在方程两边同时除以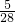 求解;
求解;

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com