
分析 如图:根据正方形对角线性质等腰直角三角形的性质作辅助虚线,图1,将等腰直角三角形分成9个相等的小三角形,正方形面积占了4份,即原面积的$\frac{4}{9}$,图2,将等腰直角三角形分成,4个相等的小三角形,正方形面积占了份,即原面积的$\frac{1}{2}$,据此解答.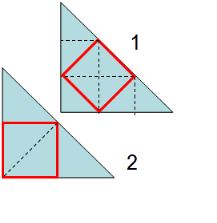
解答 解:36×$\frac{4}{9}$=16(平方厘米)
36×$\frac{1}{2}$=18(平方厘米)
答:正方形的面积是16平方厘米或18平方厘米.
点评 此题主要根据正方形对角线性质等腰直角三角形的性质,通过作辅助虚线,求出正方形与三角形面积之间的关系.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com