


科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源:数学教研室 题型:039
(
带分数,先填整数部分,再填分子,最后填分母)有一个带分数,它的整数部分和分数部分的分子、分母是三个连续的自然数,把这个带分数化成假分数后,它的分子是
11.这个带分数是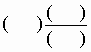 ?
?查看答案和解析>>
科目:小学数学 来源: 题型:041
(
带分数,先填整数部分,再填分子,最后填分母)有一个带分数,它的整数部分和分数部分的分子、分母是三个连续的自然数,把这个带分数化成假分数后,它的分子是
11.这个带分数是 ?
?查看答案和解析>>
科目:小学数学 来源:专项题 题型:解答题
查看答案和解析>>
科目:小学数学 来源:专项题 题型:判断题
 -
- )=6×
)=6× -6×
-6×
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com