Question

按要求画图．

（1）在上面的方格图中依次标出点A（4，5）、B（6，3）、C（9，6），连接AB、AC、BC，得到三角形ABC，这个三角形是________三角形．
（2）如果每个方格的边长是1厘米，这个三角形的面积是________平方厘米．
（3）将三角形ABC绕B点顺时针旋转90度，画出旋转后的图形．
（4）在方格图中画一个面积是12平方厘米的等腰梯形．

Answer 1

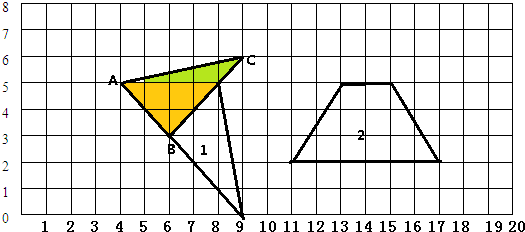
解：（1）根据数对表示位置的方法，在平面图中标出A、B、C的位置，即可得出三角形ABC，这是一个直角三角形；
（2）这个三角形的面积为：4×1÷2+4×2÷2=2+4=6（平方厘米）；
（3）把与AB、BC顺时针旋转90°，再把第三条边连接起来，即可得出旋转后的三角形1；
（4）根据图中的方格边长特点，画出上底为2厘米，下底为6厘米，高为3厘米的等腰梯形，它的面积是：（2+6）×4÷2=12（平方厘米），如图所示：

故答案为：（1）直角三角形；（2）6．
分析：（1）数对表示位置的方法是：第一个数字表示列，第二个数字表示行，由此即可解决问题；
（2）利用方格的方格的边长，将三角形分成2部分计算：上面是底为4厘米，高为1厘米的三角形；下面是底为4厘米，高为2厘米的三角形，由此即可求得三角形ABC的面积；
（3）根据旋转的性质，抓住与B相连的两条边进行顺时针旋转90°即可确定三角形的位置；
（4）根据图中方格，可以画出上底为2厘米，下底为6厘米，高为3厘米的等腰梯形，根据梯形的面积公式可知它的面积是12平方厘米．
点评：此题考查了数对表示位置的方法，图形旋转的性质，以及利用格点求图形的面积和画指定面积的图形的方法的综合应用．