
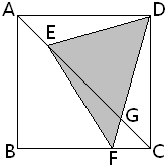
 正方形ABCD,边长为8,AE=1/4AC,CF=1/4BC,求阴影DEF的面积=
正方形ABCD,边长为8,AE=1/4AC,CF=1/4BC,求阴影DEF的面积=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:小学数学 来源: 题型:
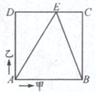 如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大
如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com