
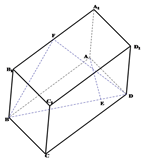
【题目】如图,已知长方体![]() ,
, ![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
, ![]() 垂直
垂直![]() 于点
于点![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 点位置;若不存在,说明理由.
点位置;若不存在,说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() ,为
,为![]() 的中点.
的中点.
【解析】试题分析:(1)先利用直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求得
,求得![]() , 以
, 以![]() 为正交基底建立平面直角坐标系,求出直线
为正交基底建立平面直角坐标系,求出直线![]() 的方向向量,利用向量垂直数量积为零列方程组求出平面
的方向向量,利用向量垂直数量积为零列方程组求出平面![]() 的一个法向量,利用空间向量夹角余弦公式可得结果;(2)令
的一个法向量,利用空间向量夹角余弦公式可得结果;(2)令![]() ,则
,则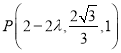 ,求出面
,求出面![]() 的一个法向量,利用(1)中平面
的一个法向量,利用(1)中平面![]() 的一个法向量,根据空间向量夹角余弦公式可得结果.
的一个法向量,根据空间向量夹角余弦公式可得结果.
试题解析:由![]() , 得
, 得 ![]() 与面
与面![]() 所成角为
所成角为![]() ,
, ![]() ,由
,由![]() ,
,
(1)以![]() 为正交基底建立平面直角坐标系,则
为正交基底建立平面直角坐标系,则
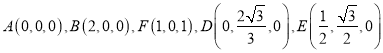 ,
, 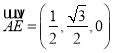 ,设面
,设面![]() 的一个法向量为
的一个法向量为![]()
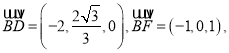
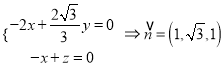
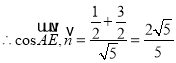
答: ![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]()
(2)令![]() ,则
,则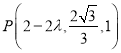
设面![]() 的一个法向量为
的一个法向量为![]() ,
, 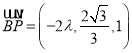
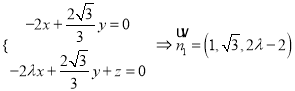
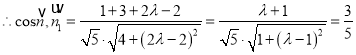
化简得![]()
![]()
答:存在点![]() ,为
,为![]() 的中点.
的中点.
【方法点晴】本题主要考查利用空间向量求线面角与二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:小学数学 来源: 题型:
【题目】列式计算
(1)一个数的5倍是280,这个数的8倍是多少?
(2)一个数比360的2倍少36,这个数是多少?
(3)8除157与141的差,商是多少?
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】计算下列各题。
(1)9×9=_____ (2)63÷9=_____ (3)64÷8=_____
(4)3×6=_____ (5)100-60=_____ (6)3×9=_____
(7)45-8=_____ (8)6×7=_____ (9)52-9=_____
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】下面的图形中哪些是直线?哪些是射线?哪些是线段?它们有什么区别和联系?(按序号的先后顺序来填写)
|
|
|
|
1 | 2 | 3 | 4 |
|
|
| |
5 | 6 | 7 |
直线:________
射线:________、________、________
线段:________、________
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】已知一条直线和直线外的A、B两点,以A、B两点和直线上某一点为三角形的三个顶点,能画出一个等腰三角形,如图中的等腰三角形ABC.除此以个最多还能画出符合条件的( )个等腰三角形.
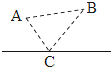
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com