Question

计算如图的表面积和体积（单位：厘米）

Answer 1

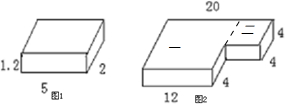
分析：图1是长方体，运用长方体的表面积=（长×宽+长×高+宽×高）×2，长方体的体积=长×宽×高，代入数据计算即；
图2是不规则的图形，添上一条线分成两个长方体（见下图），先求出完整的长方体（一）的表面积，再求出长方体（二）的上、下与前、后4个面的面积和，进而求得这个组合图形的表面积．
据此解答即可．

解答：解：图1，表面积（5×2+5×1.2+2×1.2）×2，
=（10+6+2.4）×2，
=18.4×2，
=36.8（平方厘米）；
体积：5×2×1.2=12（立方厘米）．
答：图1的表面积是36.8平方厘米，体积是12立方厘米．

图2分成两部分：图一表面积：
宽：4+4=8（厘米），
（12×8+12×4+8×4）×2，
=（96+48+32）×2，
=352（平方厘米）；
图二的表面积：长20-12=8（厘米），
（8×4+8×4）×2，
=64×2，
=128（平方厘米），
组合图形的面积：352+128=480（平方厘米），
图一的体积：12×8×4=384（立方厘米），
图二的体积：8×4×4=128（立方厘米），
组合图形的体积：384+128=512（立方厘米）．
答；图二的表面积是480平方厘米，体积是512立方厘米．

点评：此题考查规则图形的表面积和体积，解决此题的关键是把图二添一条线，分成两个长方体，进而问题得解．