画一个边长4厘米的正方形.
(1)在正方形中画一个最大的圆.(在图上要画出你是怎样找到圆心的?)
(2)如果在这个正方形中,把圆剪掉,余下部分的面积是多少?(列式计算)
(3)余下部分有______条对称轴.
解:(1)以正方形的对角线的交点为圆心,正方形边长的一半为半径,
所画出的圆就是正方形中最大的圆;
(2)余下部分的面积:4×4-3.14×
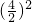
,
=16-3.14×4,
=16-12.56,
=3.44(平方厘米);
(3)沿余下部分两组对边的中线以及两条对角线所在的直线对折,对折后的两部分都能完全重合,
则余下的部分是轴对称图形,两组对边的中线以及两条对角线所在的直线就是其对称轴,
所以余下的部分有4条对称轴.
答:余下部分的面积是3.44平方厘米.

故答案为:4.
分析:(1)这个最大圆的圆心是正方形对角线的交点,半径是正方形边长的一半,从而可以画出这个最大的圆.
(2)用正方形的面积减去圆的面积,就是余下部分的面积.
(3)依据轴对称图形的概念及特征,即可判定余下部分的对称轴的条数.
点评:(1)确定出圆心的位置以及半径的长度,即可画出符合要求的圆;
(2)余下部分的面积=正方形的面积-圆的面积;
(3)解答此题的主要依据是:轴对称图形的概念、特征及其对称轴的条数.

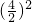 ,
, 故答案为:4.
故答案为:4.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
