
 如图,是一片刚刚收割过的稻田,每个小正方形的边长是1米,A、B、C三点周围的阴影部分是圆形的水洼.一只小鸟飞来飞去,四处觅食,它最初停留在0号位,过了一会儿,它跃过水洼,飞到关于A点对称的1号位;不久,它又飞到关于B点对称的2号位;接着,它飞到关于C点对称的3号位,再飞到关于A点对称的4号位,…,如此继续,一直对称地飞下去.由此推断,2004号位和0号位之间的距离是
如图,是一片刚刚收割过的稻田,每个小正方形的边长是1米,A、B、C三点周围的阴影部分是圆形的水洼.一只小鸟飞来飞去,四处觅食,它最初停留在0号位,过了一会儿,它跃过水洼,飞到关于A点对称的1号位;不久,它又飞到关于B点对称的2号位;接着,它飞到关于C点对称的3号位,再飞到关于A点对称的4号位,…,如此继续,一直对称地飞下去.由此推断,2004号位和0号位之间的距离是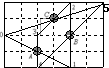


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com