练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    图中共有
     
    个正方形．
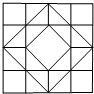
    考点：组合图形的计数
    专题：几何的计算与计数专题
    分析：先分别数出边长为1的正方形的个数；边长为边长为1的正方形对角线的正方形的个数；边长为2的正方形的个数；边长为边长为2的正方形对角线的正方形的个数；边长为3的正方形的个数；边长为4的正方形的个数；再把它们相加即可求解．
    解答： 解：边长为1的正方形有12个；
    边长为边长为1的正方形对角线的正方形有1个；
    边长为2的正方形有1个；
    边长为边长为2的正方形对角线的正方形有1个；
    边长为3的正方形有4个；
    边长为4的正方形有1个；
    12+1+1+1+4+1=20．
    答：共有20个正方形．
    故答案为：20．
    点评：考查了组合图形的计数，主要利用正方性的性质，边长相等，按一定的规律数出即可．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

    小克做了9张试卷，每张试卷的满分都是100分．小克9张试卷的平均分时68分．如果不计他的最低分，那么其他8张试卷的平均分最高是
     
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    一个四位数，给它加上小数点后，再与原数相加，和是1930.11，这个四位数是
     
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    圆周上有8个点，任意两点用线段连接，那么这些线段在圆内最多有
     
    个交点．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    如图，用火柴棒横排正方形，如果使用70根火柴棒，那么可排出
     
     个正方形．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    两数相除商9余4，如果被除数、除数都扩大到原来的3倍，那么被除数、除数、商、余之和等于333，则原来的被除数是
     
    ，除数是
     
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    李老师计划为参加数学爱好者冬令营的同学安排若干件教室．营员们到来之后，李老师发现，按照原先的计划，每间宿舍住的营员人数不全是同样多．他一计算，如果增加 2间宿舍，每间宿舍恰好住 6 人；如果减少 2 间宿舍，每间宿舍恰好住 9 人．参加冬令营的营员共有
     
    人．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    如图，CDEF为正方形，ABCD是等腰梯形，上底AD=23，下底BD=35，则△ADE的面积为
     
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    两个正方形的边长比是1：2，那么这两个正方形的面积比是（　　）
    A、1：2B、1：4
    C、4：1D、2：1

    查看答案和解析>>

    同步练习册答案