解:(1)0.34×12.5+0.125+66,
=0.34×12.5+12.5×0.66,
=(0.34+0.66)×12.5,
=1×12.5,
=12.5;
(2)103×0.3,
=(100+3)×0.3,
=100×0.3+3×0.3,
=30+0.9,
=30.9;
(3)4.34÷0.25÷4,
=4.34÷(0.25×4),
=4.34÷1,
=4.34;
(4)130130÷11111×66666,
=130130÷11111×11111×6,
=130130×6,
=780780;
(5)40.5×1.1-4.05,
=4.05×11-4.05,
=4.05×(11-1),
=4.05×10,
=40.5;
(6)100-98+96-94+92-90+…+8-6+4-2,
=(100-98)+(96-94)+(92-90)+…+(8-6)+(4-2),
=2×(100÷2÷2),
=2×25,
=50;
分析:(1)原式化成0.34×12.5+12.5×0.66,运用乘法的分配律进行简算,
(2)把103化成100+3,再运用乘法的分配律进行简算,
(3)运用除法的性质进行计算即可,
(4)原式化成130130÷11111×11111×6,再进行计算即可,
(5)运用乘法的分配律进行简算,
(6)算式中的数字是100以内的所有偶数,共50个,每两个偶数的差为2,因此2×(50÷2)计算即可.
点评:完成此题,注意合理分组以及数字转化,巧妙灵活地运用运算技巧或定律,进行简算即可.



 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案 =________
=________ +
+ =________
=________ -
- =________
=________ ×
×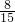 =________
=________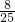 ÷
÷ =________
=________