
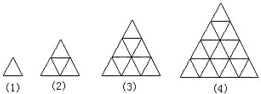
 如图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:
如图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:分析 (1)第一个图形的最下面一层是1个三角形,第二个图形最下面的一层是1+2个三角形,第三个图形最下面的一层是1+2+3个三角形,…则第n个图形的最下面的一层就是1+2+3+…+n个三角形,据此即可 解答问题.
(2)第一个图形有1层,有1=12个三角形,第二个图形有2层,有1+3=22个三角形,第三个图形有3层,有1+3+5=32个三角形,第三个图形有4层,有1+3+5+7=42个三角形,据此推测第n个图形有n层,有1+3+5+7+…+(2n-1)=n2个三角形.
解答 解:(1)1+2+3+4+5=15
15+6=21
21+7=28
第n个图形的最下面的一层就是1+2+3+…+n个三角形.
答:五层的“宝塔”最下层包含15个小三角形,六层有21个,七层有28个,n层有1+2+3+…+n个.
(2)52=25
62=36
72=49
第n个图形有n层,有1+3+5+7+…+(2n-1)=n2个三角形.
答:整个五层“宝塔”一共包含25个小三角形,六层有26个,七层有49个,n层有n2个.
点评 解答本题的关键是:根据图形及其数列的变化规律求解即可.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com