
分析 6个人所需要的时间分别是5分钟、4分钟、3分钟、10分钟、7分钟、6分钟,按顺序分别记作①、②、③、④、⑤、⑥,要使等候的时间最少,需要让用时最少的先打,因为3<4<5<6<7<10,所以按③→②→①→⑥→⑤→④的顺序打水使等侯的时间和最少;据此解答.
这时当③打水时,需要6人等候,②打水时需要5个人等候,当①打水时需要4个人等候,当⑥打水时需要3个人等候,当⑤打水时需要2个人等候,当④打水时需要1个人等候,等侯时间的总和为:3×6+4×5+5×4+6×3+7×2+10=100(分钟),据此解答.
解答 解:根据题干分析可得:6个人所需要的时间分别是5分钟、4分钟、3分钟、10分钟、7分钟、6分钟,
按顺序分别记作①、②、③、④、⑤、⑥,
要使等候的时间最少,需要让用时最少的先打,
因为3<4<5<6<7<10,所以按③→②→①→⑥→⑤→④的顺序打水使等侯的时间和最少;
等侯时间的总和为:3×6+4×5+5×4+6×3+7×2+10=100(分钟),
答:要使等候的时间最少,需要让用时最少的先打,这个最短的时间是 100分钟.
故答案为:100.
点评 本题实际是统筹优化问题,因为等候的总时间与等候的人数和每人需要的时间有关,在人数不变的情况下,需要让用时最少的先接水.


科目:小学数学 来源: 题型:计算题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:计算题
| 225+475= | 19.3-2.7= | $\frac{2}{3}$+$\frac{1}{3}$= | 1÷1.75= | $\frac{3}{4}$×$\frac{4}{3}$= |
| 5.1÷0.01= | $\frac{7}{8}$×5.6= | 8.1-6= | 4.1+1÷2= | (3.5%-0.035)÷2= |
查看答案和解析>>
科目:小学数学 来源: 题型:操作题
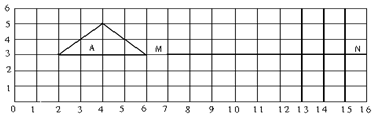
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com