Question

18．经过5个点中的每两点画直线，最多可以画10条．在图中画一画．

Answer 1

分析 根据过两点的直线有1条，过不在同一直线上的三点的直线有3条，过任何三点都不在一条直线上四点的直线有6条，按此规律，由特殊到一般，总结出规律：平面内任意三个点都不在同一直线上，平面内有n个点，一共可以画直线的条数为$\frac{1}{2}$n（n-1）．

解答 解：如图：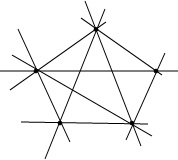

经过不在一条直线上的5个点中的每两个点，最多可以画4+3+2+1=5×4÷2=10条直线．
答：最多可以画10条直线．
故答案为：10．

点评 本题是探索规律题，有n个点，每三个点都不在一条直线上，过其中每两个点画直线，可以画$\frac{1}{2}$n（n-1）条直线．