考点:组合图形的面积
专题:平面图形的认识与计算
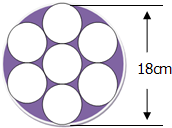
分析:观察图发现:大圆的直径与3个小圆的直径相等,大圆的直径除以3就是小圆的直径,再分别求出大圆和每个小圆的半径,根据圆的面积公式,求出大圆的面积和每个小圆的面积,然后根据阴影部分的面积=大圆的面积-7个小圆的面积进行求解.
解答:
解:18÷3=6(厘米)
18÷2=9(厘米)
6÷2=3(厘米)
3.14×92-3.14×32×7
=254.34-197.82
=56.52(平方厘米)
答:阴影部分的面积是56.52平方厘米.
点评:解决本题关键是找出小圆和大圆直径之间的关系,再根据圆的面积S=πr2进行求解.



 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案