
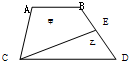
 如图,ABCD是一个梯形,E是BD的中点,线段CE把梯形分成甲、乙两部分,它们的面积之比是9:5,求上底AB与下底CD的长度之比.
如图,ABCD是一个梯形,E是BD的中点,线段CE把梯形分成甲、乙两部分,它们的面积之比是9:5,求上底AB与下底CD的长度之比.


 学习实践园地系列答案
学习实践园地系列答案科目:小学数学 来源: 题型:
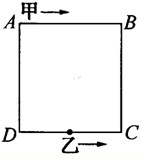 如图,ABCD是一个边长为6米的模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,乙玩具车从CD的中点出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米?
如图,ABCD是一个边长为6米的模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,乙玩具车从CD的中点出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米?查看答案和解析>>
科目:小学数学 来源: 题型:
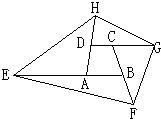 如图,ABCD是一个四边形,它的面积是1,延长BA到E,使AE=2BA;延长AD到H,使DH=AD;延长DC到G,使CG=2DC;延长CB到F,使BF=CB.那么四边形EFGH的面积是
如图,ABCD是一个四边形,它的面积是1,延长BA到E,使AE=2BA;延长AD到H,使DH=AD;延长DC到G,使CG=2DC;延长CB到F,使BF=CB.那么四边形EFGH的面积是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com