Question

3．如图，两个四分之一圆弧的半径分别是4和8，求两个阴影部分的面积之差．

Answer 1

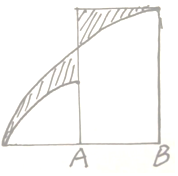
分析 观察图形可知，两个阴影部分的面积之差=半径为8的圆心角为90°的扇形面积-[长8宽（8-4）的长方形面积+半径为4的圆心角为90°的扇形面积]，根据长方形面积公式S=ab和扇形的面积公式S=$\frac{nπ{r}^{2}}{360}$列式计算即可求解．

解答 解：$\frac{90×3.14×{8}^{2}}{360}$-[8×（8-4）+$\frac{90×3.14×{4}^{2}}{360}$]
=50.24-（8×4+12.56）
=50.24-（32+12.56）
=50.24-44.56
=5.68
答：两个阴影部分的面积之差是5.68．

点评 考查了组合图形的面积，方法：①“割法”：观察图形，把图形进行分割成容易求得的图形，再进行相加减．②“补法”：观察图形，给图形补上一部分，形成一个容易求得的图形，再进行相加减．③“割补结合”：观察图形，把图形分割，再进行移补，形成一个容易求得的图形．