Question

7．将自然数1，2，3，4，5，6，7，…依如图所示之顺序排列．我们将2，3，5，7，10，…称为“拐角数”，因为指向它的箭头与离开它A箭头方向改变了．那么在529与1000之间有多少个“拐角数”？

Answer 1

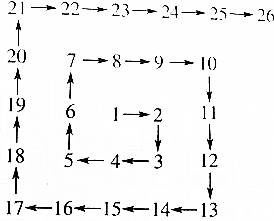
分析 观察拐弯处的数字的规律，既可以得到n个拐弯处的数字的特点，根据题干观察拐弯处的数的规律，可以得到n个拐弯处的数的规律为：
①当n为奇数时为：第1个数2=（$\frac{1+1}{2}$）²+1
第三个数5=（$\frac{3+1}{2}$）²+1
第五个数10=（$\frac{5+1}{2}$）²+1
因此可以归纳出n为奇数时的规律为（$\frac{n+1}{2}$）²+1
②同理可归纳出当n为偶数时的规律为（1+$\frac{n}{2}$）×$\frac{n}{2}$+1．
拐弯处的根据规律大体判断出从529到1000的自然数是在那几个拐弯范围之内，然后找出符合条件的数即可．

解答 解：（1）第45次拐弯处的数是（$\frac{45+1}{2}$）²+1=530．
（2）试算n=46时，拐弯处的数是（1+$\frac{46}{2}$）×$\frac{46}{2}$+1=553；
n=47时，
拐弯处的数是（$\frac{47+1}{2}$）²+1=577
n=48时，
拐弯处的数是（1+$\frac{48}{2}$）×$\frac{48}{2}$+1=601；
n=49时，
拐弯处的数是（$\frac{49+1}{2}$）²+1=626
n=50时，
拐弯处的数是（1+$\frac{50}{2}$）×$\frac{50}{2}$+1=651
n=51时，
拐弯处的数是（$\frac{51+1}{2}$）²+1=677
把拐角数两两组合：（2，3）（5，7）（10，13）（17，21）（26，31）…（651′，677）…
第N组第一个数：N²+1第二个数：N²+N+1
讨论：①22²+22=485＞500（N=22）22²+22+1=507＞500
②31²+1=962＜1000（N=31）31²+31+1=993 （31-22）×2+1=19（个）
答：在529与1000之间有19个“拐角数．

点评 从拐弯处数字入手，寻求它们的规律，然后灵活运用找出的规律解决问题．