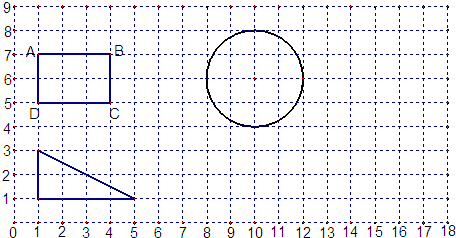
解:(1)根据旋转的性质,绕点C先将CB与CD边顺时针旋转90°,即可画出这个旋转后的长方形如图1,则旋转后A的位置为:(6,8);
(2)将圆心向右平移4格,以同样长度为半径画出圆,如图2,经过这两个圆的圆心的直线和经过两圆的切点且垂直于两圆的连心线的直线就是这个组合图形的对称轴;
(3)将直角三角形的两条直角边缩小2倍,即可画出这个缩小后的三角形,如图3,
因为这两个三角形是相似三角形,所以面积比就等于相似比的平方,即缩小后三角形的面积是原来的

.
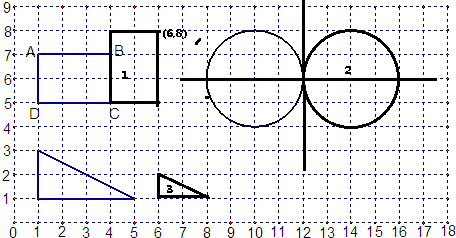
故答案为:(1)6,8;(3)

.
分析:(1)根据旋转的性质,绕点C先将CB与CD边顺时针旋转90°,由此即可确定旋转后的图形的位置与大小,再利用数对表示位置的方法即可解决问题;
(2)根据平移的性质,将圆心向右平移4格,以同样长度为半径画出圆,经过这两个圆的圆心的直线就是这个组合图形的对称轴;
(3)根据放大与缩小的性质,将直角三角形的两条直角边缩小2倍,即可画出这个缩小后的三角形,因为这两个三角形是相似三角形,所以面积比就等于相似比的平方.
点评:此题考查了图形的旋转、平移、放大与缩小的性质、轴对称图形的对称轴的画法以及数对表示位置的方法的灵活应用.

 .
.
 .
.
 .
.
