
分析 圆柱的体积=底面积×高,半径扩大1$\frac{1}{3}$倍,那么底面积就会扩大到原来的(1$\frac{1}{3}$×$1\frac{1}{3}$)=$\frac{16}{9}$倍,高缩小$\frac{3}{2}$,根据积的变化规律:一个因数不变,另一个因数扩大几倍(或缩小几倍)积就扩大(或缩小)几倍,所以圆柱的体积是原来的:$\frac{16}{9}$÷$\frac{3}{2}$=$\frac{32}{27}$倍.
解答 解:根据题干分析可得:圆柱的体积是原来的:(1$\frac{1}{3}$×1$\frac{1}{3}$)÷$\frac{3}{2}$=$\frac{32}{27}$.
答:它的体积是原来体积的$\frac{32}{27}$倍.
点评 此题考查了圆柱的体积公式与积的变化规律的综合应用.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
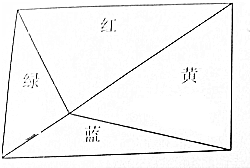 如图,一个长方形被分成4个不同的三角形,如果绿色三角形的面积是原长方形面积的$\frac{1}{5}$,黄色三角形面积是15平方厘米,那么原长方形的面积是多少平方厘米?
如图,一个长方形被分成4个不同的三角形,如果绿色三角形的面积是原长方形面积的$\frac{1}{5}$,黄色三角形面积是15平方厘米,那么原长方形的面积是多少平方厘米?查看答案和解析>>
科目:小学数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com