练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    8．学校举行写字比赛，二等奖的人数是一等奖人数的2倍，三等奖的人数是二等奖人数的2倍多12人，学校规定获奖人数不超过100人，请你画画线段图．计算出可获奖的最多人数是多少？

    分析 由题意，得二等奖的人数是得一等奖的人数的2倍，三等奖的人数是二等奖人数的2倍多12人，则获奖总人数不超过100人，先按照100人算，就是得一等奖的人数的（1+2+2+2）倍多12人，由此用除法可求得得一等奖的人数，进而计算出可获奖的最多人数是多少即可．

    解答 解：如下图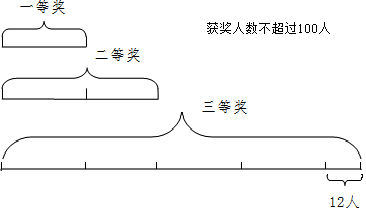

    100-12=88（人）
    88÷（1+2+4）
    =88÷7
    =12（人）…4
    所以获一等奖的是12人，那么获奖的最多人数是：
    12+12×2+12×4+12
    =84+12
    =96（人）
    答：获奖的最多人数是96人．

    点评 此题考查了和倍公式“和÷（倍数+1）=小数”的灵活运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：判断题

    18．9吨是9000千克的1倍．√．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：计算题

    19．列竖式计算．
    514+218+212         
    384+672-590           
    1000-273-135．

    查看答案和解析>>

    科目：小学数学 来源： 题型：计算题

    16．直接写出得数
    1.25+$\frac{3}{4}$=1-0.09=0×125=
    $\frac{1}{5}$÷$\frac{1}{4}$=25×0.9×4=195÷19.5-10=
    3-25%+$\frac{1}{4}$=

    查看答案和解析>>

    科目：小学数学 来源： 题型：计算题

    3．计算下面各题，能简便运算的要用简便方法计算，写出过程．
    （1）7.38×0.5÷0.3；（2）0.67×3.8+6.2×0.67．

    查看答案和解析>>

    科目：小学数学 来源： 题型：计算题

    13．根据已知条件，求a：b：c．
    $\frac{1}{a}$：$\frac{1}{b}$：$\frac{1}{c}$=2：3：5．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    20．用两个完全一样的三角形可以拼成一个平行四边形，拼成的平行四边形的底是原三角形的底，它的高是原三角形的高．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    10．填上＞、＜或=．
    0.375÷2.4=3.75÷24             
    0÷9.9＜9.9
    22÷7＞3.1414…
    2.4÷1.2＜2.4．

    查看答案和解析>>

    科目：小学数学 来源： 题型：判断题

    11．小明画了一条23分米长的直线．× （判断对错）

    查看答案和解析>>

    同步练习册答案