
分析 因为60=2×2×3×5=(2+1)×(1+1)×(1+1)×(4+1)
根据约数个数公式,所求最小的数可能是:
22 ×32×2×4×5×7=5040
则最小的有60个因数的数就是5040.
解答 解:60=2×2×3×5=(2+1)×(1+1)×(1+1)×(4+1)
根据约数个数公式,所求最小的数可能是:
22 ×32×2×4×5×7=5040
则最小的有60个因数的数就是5040.
故答案为:5040.
点评 此题考查了约数和定理的灵活应用:一个合数分解质因数为:p1m×p2n×…×pkq,则这个合数的因数个数为:(m+1)×(n+1)×…×(q+1).


科目:小学数学 来源: 题型:解答题
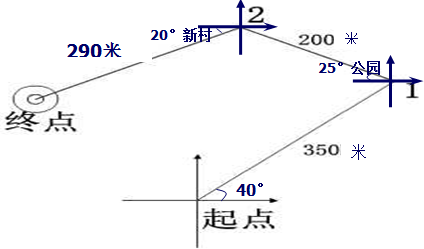
| 方 向 | 时 间 | 路 程 | |
| 起点→公园 | 5分钟 | ||
| 公园→新村 | 3分钟 | ||
| 新村→终点 | 4分钟 |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
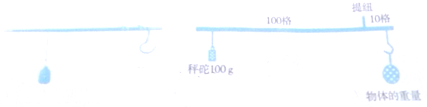
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com