
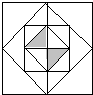
 将边长为a的正方形各边的中点连接成第二个正方形,再将第二个正方形各边的中点连接成第三个正方形,依此规律,继续下去,得到图xx0402_02.那么,边长为a的正方形面积是图中阴影部分面积的________ 倍.
将边长为a的正方形各边的中点连接成第二个正方形,再将第二个正方形各边的中点连接成第三个正方形,依此规律,继续下去,得到图xx0402_02.那么,边长为a的正方形面积是图中阴影部分面积的________ 倍.

科目:小学数学 来源: 题型:
 将边长为a的正方形各边的中点连接成第二个正方形,再将第二个正方形各边的中点连接成第三个正方形,依此规律,继续下去,得到图xx0402_02.那么,边长为a的正方形面积是图中阴影部分面积的
将边长为a的正方形各边的中点连接成第二个正方形,再将第二个正方形各边的中点连接成第三个正方形,依此规律,继续下去,得到图xx0402_02.那么,边长为a的正方形面积是图中阴影部分面积的查看答案和解析>>
科目:小学数学 来源: 题型:
 将边长为正整数n的正方形平均分成n2个小正方形,每个小正方形的顶点称为格点.例如:图A中的格点是边长为2的正方形的格点.图B中,在边长为12的正方形中有四个完全相同的直角三角形.如果三角形的一条直角边是3,那么这四个三角形各边共经过多少个格点?(每个格点只计一次)
将边长为正整数n的正方形平均分成n2个小正方形,每个小正方形的顶点称为格点.例如:图A中的格点是边长为2的正方形的格点.图B中,在边长为12的正方形中有四个完全相同的直角三角形.如果三角形的一条直角边是3,那么这四个三角形各边共经过多少个格点?(每个格点只计一次)查看答案和解析>>
科目:小学数学 来源: 题型:
 一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).
一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).
一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com