
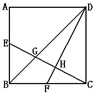
 正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,四边形BGHF的面积是多少平方厘米?
正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,四边形BGHF的面积是多少平方厘米? S正ABCD=
S正ABCD= ×120=30平方厘米,
×120=30平方厘米, S正ABCD=
S正ABCD= ×120=30平方厘米,连接GF,F是BC的中点,则S△GBF=S△GFC,
×120=30平方厘米,连接GF,F是BC的中点,则S△GBF=S△GFC,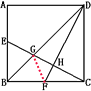


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:小学数学 来源: 题型:
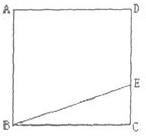 E是正方形ABCD的边CD上的三等分点(如图),BE把正方形分成一个梯形和一个三角形.梯形的周长比三角形的周长大8厘米.正方形ABCD的面积是
E是正方形ABCD的边CD上的三等分点(如图),BE把正方形分成一个梯形和一个三角形.梯形的周长比三角形的周长大8厘米.正方形ABCD的面积是查看答案和解析>>
科目:小学数学 来源: 题型:
 [化整为零].如图,正方形ABCD和正方形EFGH分别内接于同一个等腰直角三角形MBN(这里的内接指正方形的四个顶点全部在三角形的边上).已知正方形ABCD的面积是72平方厘米,那么正方形EFGH的面积是多少平方厘米?
[化整为零].如图,正方形ABCD和正方形EFGH分别内接于同一个等腰直角三角形MBN(这里的内接指正方形的四个顶点全部在三角形的边上).已知正方形ABCD的面积是72平方厘米,那么正方形EFGH的面积是多少平方厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com